Edge Physics and Non-Abelian Statistics
The fractional quantum Hall (FQH) effect emerges in a highly interacting two-dimensional electron gas at high magnetic field and ultralow temperature. In FQH effect, there is a quantized Hall resistance which is h/e2 divided by a fraction. The first fraction is 1/3 and many more fractions have been observed so far. Most of them are odd denominator fractions and these FQH states can be explained by the composite fermion theory.
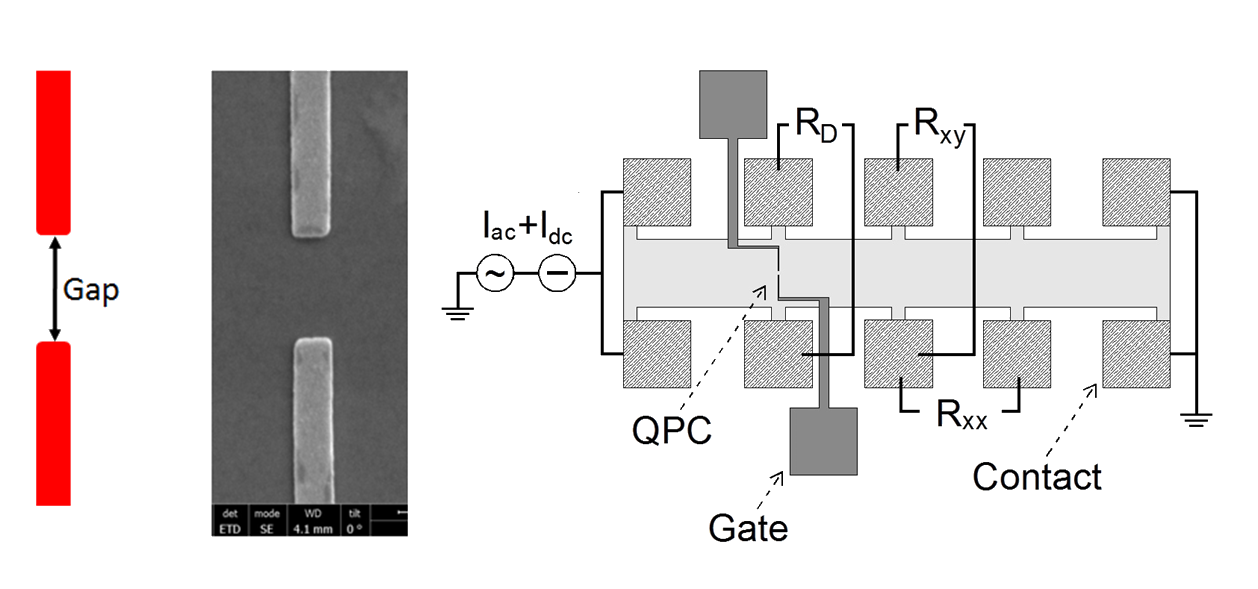
FQH states have gapless conducting edge currents at the boundaries, in which fractionally charged quasi-particles carry the current. If the counter-propagating edge currents of a FQH state are brought close enough together in a quantum point contact (QPC), tunneling of quasi-particles is induced. If multiple QPCs are used, interferometer can be constructed. Through measurements in single QPC or multiple QPCs, the edge physics of FQH states can be studied. Similar techniques may be extended to other systems with edge states.
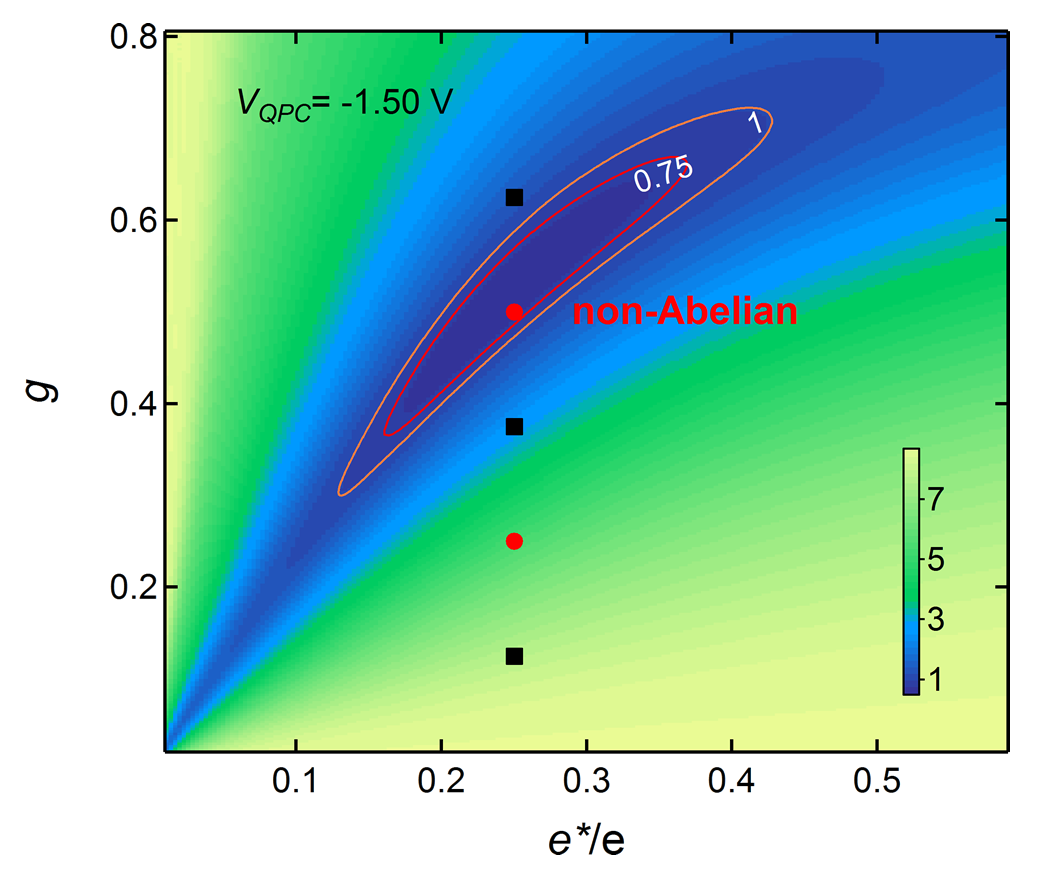
The 5/2 FQH state is special because it is an even-denominator state with elementary excitations that may have non-Abelian statistics, where statistics means the property of wave function under exchange of indistinguishable quasi-particles. The exchange of Bosons or Fermions only generates a zero or π phase factor in the wave function, but in non-Abelian statistics, interchange of particles can change the wave function more than just a phase shift. As a result, non-Abelian statistics is a candidate for fault-tolerant topological quantum computation. The property of the statistics and other interesting phenomena with quasi-particles can be probed through edge physics. An introductory review of related experimental progress can be found in National Science Review 1, 564 (2014) .
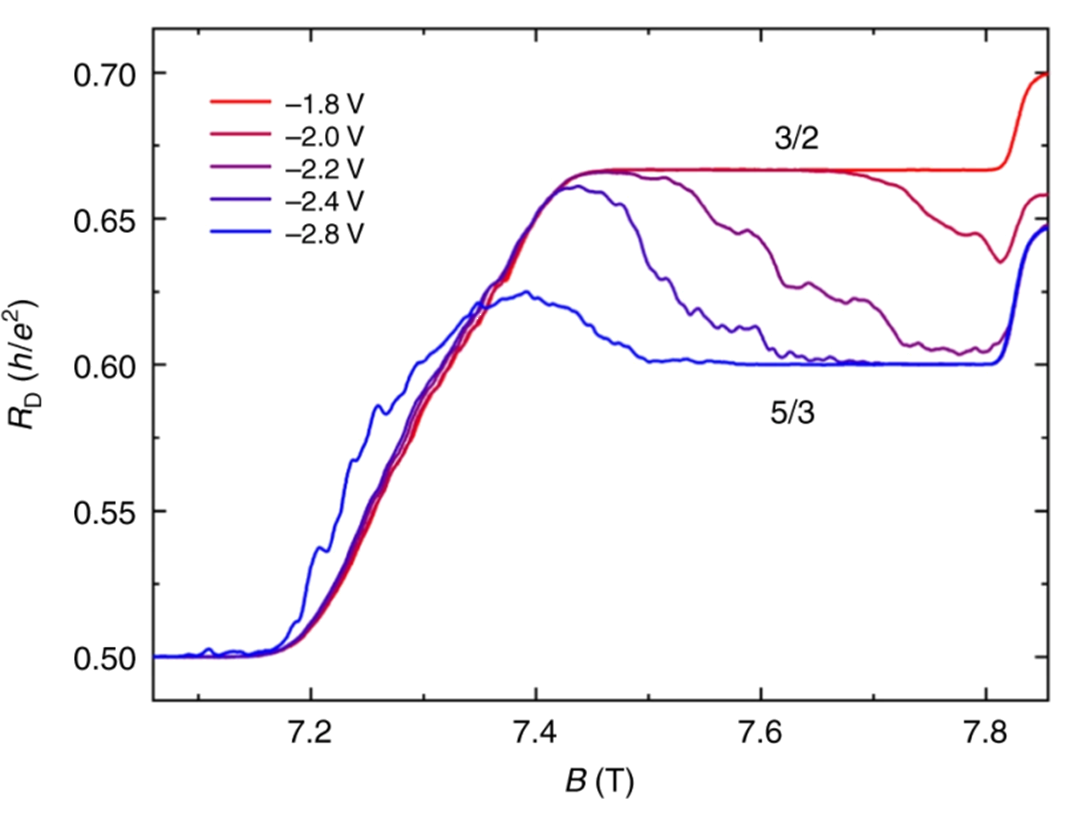
By confining two-dimensional electrons with appropriate boundary potential, we successfully induced a 3/2 fractional quantum Hall plateau in single layer two-dimensional electron gas. The conductance transmitting through the confined region is also quantized at 3/2 e2/h, and a conductance of 1/6 e2/h is backscattered. A 3/2 fractional quantum Hall state at the first Landau level is unexpected from either the framework of composite fermion or the current understanding of even-denominator states. Further charge fractionalization of quasi-particles through topological defect is proposed as a promising explanation for this unexpected quantization, resulting in a new elemental excitation with e/6 fractional charge.